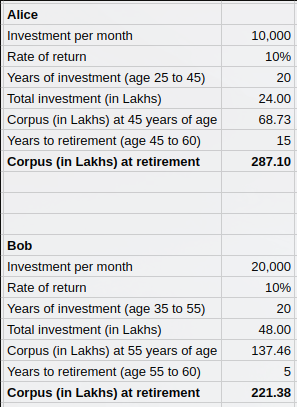Math Behind Financial Planning (FV, PV and Annuity)
Saving early is one of the first steps you need to take when you are planning early retirement. I talked about it briefly in my earlier post, but wanted to elaborate a little bit and may be show a few formulas along the way to help you better understand how starting early and compounding make such a huge difference. This post will help you do your own financial planning if you are so inclined. I did not use a financial planner and always preferred to do it myself. So if you are like me, you might enjoy it.
Let’s start with the Alice and Bob’s story once again and figure out how we arrived at the numbers we did. The story goes like this – Alice and Bob are the same age and get their job at the same time when they are 25 years old. Alice starts investing Rs. 10,000 from the age of 25 to 45 and then stops investing until her retirement at 60. Bob on the other hand spends all his income in his initial years and does not start investing until the age of 35. He then starts investing Rs. 20,000 (twice the amount of Alice) for 20 years just like Alice. Then he stops investing and retires at 60 like Alice. In the end Alice retires with Rs. 2.87 crores while Bob retires with Rs. 2.21 crores.
Now for the math. When you are doing financial planning you should learn the basics of Future Value (FV) and Present Value (PV). They help in knowing the value of money as we move through time, aka time value of money. For the sake of simplicity, let us assume that the investments compound only annually (and not monthly). Then the total investment made by Alice in the first year is Rs. 1,20,000. So what is the value of it in 20 years if the annual return on investment is 10%? Going back to our basic school math on compound interest, we figure it to be Rs. 8,07,300.
Amount = Principle * (1 + Rate of Return as decimal) ^ Number of Years
Amount = 1,20,000 * (1 + 0.1) ^ 20 = 8,07,300
That is the Future Value. So the Future Value of first year’s investment is Rs. 8,07,300. Likewise the Present Value of Rs. 8,07,300 is Rs. 1,20,000. The Present Value is also useful to figure out what your future income can buy you in today’s terms. For example if you were to receive a Rs. 50,000 monthly income 20 years from now, what would be your purchasing power? Let’s continue further with the example, so Rs. 50,000 per month is Rs. 6,00,000 annually. And assuming an inflation of 6%, we run through the formula again.
FV = PV * (1 + rate) ^ time
6,00,000 = PV * (1 + 0.06) ^ 20
PV = 6,00,000 / (1 + 0.06) ^ 20 = 1,87,083 = 15,590 per month
So, with Rs. 50,000, some 20 years later, you can only buy today’s Rs. 15,590 worth of things. This hopefully helps you visualize the power of compounding.
The next important concept to learn is annuities. Remember how we calculated that the future value of Rs. 1,20,000 for Alice? What if we wanted to calculate the total amount accrued over the next 20 years of her investment? The first year she invests Rs. 1.2 L, the value of which 20 years later is 1.2 * (1 + 0.1)^20 = Rs. 8.07L. Next year she invests another Rs. 1.2L, the value of which 19 years later is 1.2 * (1 + 0.1)^19 = Rs. 7.34L. The next year’s Rs. 1.2L becomes 1.2 * (1 + 0.1)^18 = Rs. 6.67L after 18 years and so on. To find the total corpus for Alice after 20 years we need to add all these 20 future values. That is a lot of work. There is actually a simpler formula to calculate the sum of future values of such periodic investments and it is called annuity. With some help from Geometric Series we get
Annuity = a * (1 + r)^n + a * (1 + r)^(n−1) + ⋯ + a * (1 + r)^2 + a * (1 + r) + a
Replacing (1 + r) with i we get
Annuity = a * i^n + a * i^(n−1) + ⋯ + a * i^2 + a * i + a
Re-arranging the numbers (reversing the summation)
Annuity = a + a * i + a * i^2 + ⋯ + a * i^(n-1) + a * i^n
Annuity = a * (1 - i^n) / (1 - i) [solving with Geometric Series]
Annuity = a * ((1 + r) ^ n - 1) / r [Replacing i with (1 + r)]
Thankfully, in this day and age, you don’t have to put so much effort. Just open a Spreadsheet and type in this formula in a cell to calculate annuity without all the math
= FV(rate, number of periods, payment amount, 0)
= FV(10%, 20, 120000, 0) = 68.73 Lakhs
So after 20 years Alice has Rs. 68.73 lakhs. Continuing further, we want to find the amount she would have after 15 years when she retires. Which is basically the future value of Rs. 68.73.
FV = 68.73 * (1 + 0.1)^15 = 2.87 Cr
We can do the same for Bob and arrive at these numbers.
If you would like to learn more about PV, FV and annuities, try out this excellent course that I took a while ago. It is a very easy to understand and well taught course. You may like these other classes that I took in the past
Of course, if you rather not do all the math then there are tons of online calculators that do the job for you. I have a few of those calculators on this blog.